申探社：不确定度建模（中）-蒙特卡洛采样

在（上）篇中，我们讨论了什么是不确定度，为什么需要关注不确定度建模，以及不确定度可以怎么用。也从最大似然估计（MLE）到最大后验概率（MAP），讲到了贝叶斯推断(Bayesian Inference)。而我们希望用来建模不确定的目标模型是贝叶斯神经网络（BNN），它是一种用神经网络来建模似然率，然后进行贝叶斯推断的方法。（中）篇会介绍如何用蒙特卡洛采样的方法来进行贝叶斯推断。主要是概念图中的这一部分：

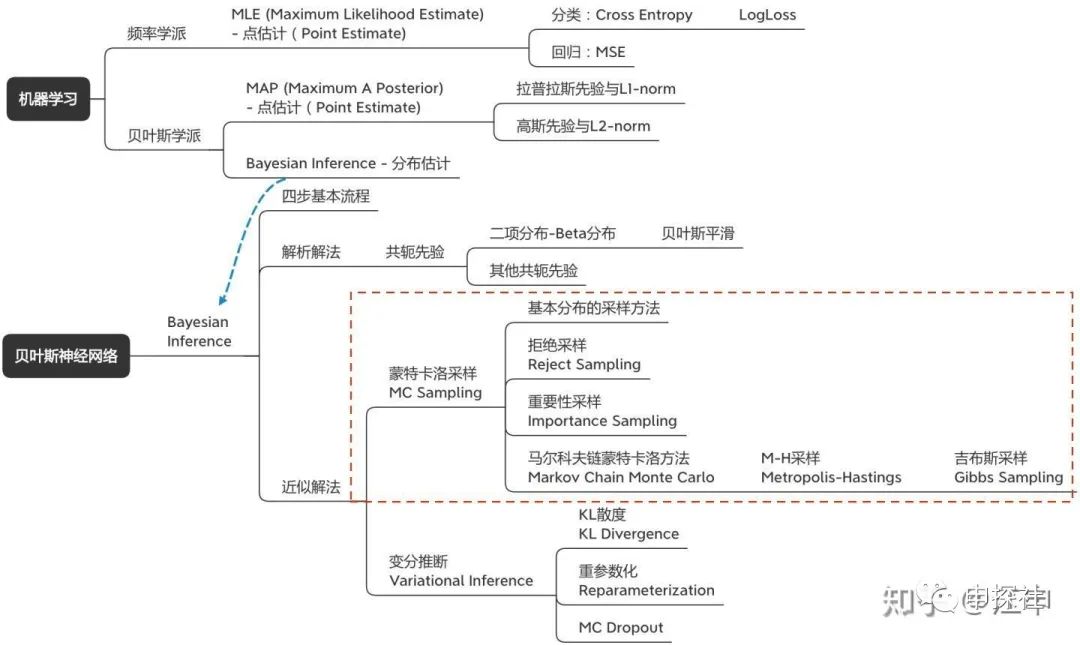
回顾一下，贝叶斯推断通常遵循以下的四步：

第一步：假设先验  ，对似然率建模 
第二步：计算后验 
展开后有 
第三步：计算预测值的分布 
第四步：计算y的期望值  ；
如果需要，计算y的方差  作为预估值的不确定度

通常我们很容易的可以把后验分布的表达式  写出来，但是到第三步，是一个积分，这里就比较麻烦了。如果我们选择的似然率的模型和先验模型不是刚好有些特殊性质可以利用，很难直接把积分求出来。另外第四步里也需要用积分来求期望值（或者方差）。

如果不追求精确的解析解，而可以接受近似解的话，有两个方法可以解决这个问题：一个是蒙特卡洛采样，一个是变分推断。

一、蒙特卡洛采样

我们先来看蒙特卡洛采样的方法。拉斯维加斯，澳门，都是世界著名赌城，还有另外一座城市，和它们并称“世界三大赌城”。这个城市的名字就叫做蒙特卡洛，这个算法的名字也就起源于这个城市。

如果我们是蒙特卡洛赌城的老板，我们需要设计一台老虎机，怎么做可以知道这台老虎机是不是稳赚不赔的？一个最简单的方法就是找一批测试人员轮流模拟玩家在这台机器上试玩1000次，看看最终机器是不是赚钱了，赚了多少钱，然后再除以1000，得到的就是玩家平均每玩一次赌场赚的钱。这个叫做老虎机的ev（expected value）。赌场的机器，对于玩家来说都是负ev的。所以长期玩下去，赌场肯定是赚的。

这种求单次赌场平均盈利的方法，就是蒙特卡洛采样法。更通用地来说，蒙特卡洛采样法是指用从一个分布中采样很多样本，然后用这些样本来代替这个分布进行相关计算（例如求期望值）的方法。比如说我们要下面这个积分

回顾一下期望值计算公式，上式其实就是当x的分布为  时，的期望值。

如果我们不能直接把积分的解析解算出来，就可以用蒙特卡洛采样的方法，从 中采样很多样本  （类比赌场找来的测试人员）然后把这些样本带入  （类比测试人员去玩一次老虎机），得到（类比测试人员玩老虎机的盈亏）再把他们的均值算出来就得到了这个积分的一个近似解（类比老虎机的ev）。采样的样本越多，得到的解越接近解析解（大数定律）

我们先回到贝叶斯推断里关键的第三步和第四步，把第三步的分布带入到第四步的期望值公式里，则有  。因为y与  无关，可以放到第二个积分内部，则有。再调整下积分的顺序，并把与y无关的  挪到外面，则有 

上式中，我们会发现括号内的积分，其实就是 的均值。在大多数时候，我们在对似然率建模的时候，会间接通过对均值建模来实现。例如在回归问题里，神经网络的输出作为高斯分布的均值来建模似然率，即  ，其中  表示神经网络的输入和参数，  表示神经网络的输出值，也是高斯分布的均值。 一般是个超参数。如果是分类问题，则神经网络的输出会作为伯努利分布里的y=1的概率，也是伯努利分布的均值。所以上面的式子就变成 

所以，利用蒙特卡洛采样的方法，如果我们能从  分布里采样很多  ，然后分别带入到里算出神经网络的一系列输出值，再求均值，也就是最终我们要的  了。

那么现在的问题就变成：我们如何根据一个分布的表达式（在这里主要是指），从这个分布中采样出很多样本来。（采样问题）

另外一个问题是，我们要采样的分布  里，有一个积分，这个积分也很不好算（归一化问题）。不过它是作为一个归一化分母来使用的，如果我们能在采样的时候，有办法忽略这个归一化分母就好了。大家记住这个问题，后面我们会多次提到怎么来化解。

二、基本分布的采样方法

对于均匀分布，我们可以用随机数发生器很容易的采样出来。借助随机数发生器，我们可以实现另外一些简单的分布，例如伯努利分布，用简单的if else就可以实现；也可以实现稍微复杂一些的分布，比如高斯分布，可以借助Box-Muller方法来实现：

Box-Muller方法：选取两个服从[0,1]上均匀分布的随机变量U1，U2，则X，Y为均值为0，方差为1的高斯分布，且X，Y独立。

因为不是本文重点，不展开证明。

但是对于更复杂的分布，采样就变得并不容易了。有一系列采样算法来帮助我们通过上面介绍的这些基本分布的采样方法，来实现从我们想要的分布中去采样样本。

三、复杂分布的采样算法

1. 拒绝采样

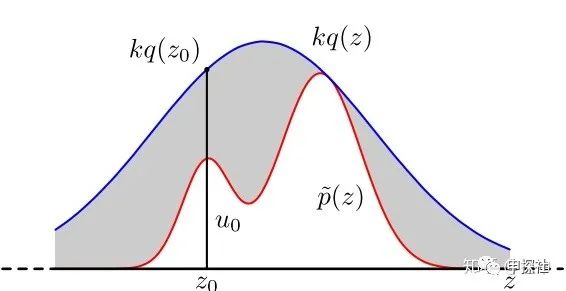
假设如果我们开了一家饭店，开业大酬宾搞了一个促销活动，来吃饭的人只要扔一次骰子，如果扔6就能享受免单。那么免单概率是1/6。如果我们发现这样下去要亏本，想把免单概率调整为1/12怎么办？那么我们可以修改规则为对扔到6的人，随机一半概率才能免单，就可以把概率变为1/12了。具体实施方式为，要求扔到6的人，再扔一次硬币，如果是反面，则我们拒绝免单，如果是正面，我们接受免单。这样就达到了以1/12概率采样的效果。

拒绝采样也是类似的思想。假设我们已经能从分布q中采样样本（这个分布也叫Proposal Distribution，例如一个高斯分布），而我们的目标是要对目标分布 p去采样。

在一开始，我们先对两个分布都做一个变换。先把p分布乘以一个归一化分母  （是个常数），得到  。回顾上面说的  有一个归一化分母不好计算的问题，而做拒绝采样只需要用到  ，因此就不需要考虑归一化分母计算的问题了。然后我们再对分布q的概率密度函数乘以一个常数k，使得新的概率密度函数始终在的上方，也就是让蓝线始终在红线上方或者和红线重合。

然后我们从分布q中进行采样，假设我们采样出的样本是  ，它对应的放大后的q分布的概率密度值是  ，它对应的目标分布的概率密度是  ，那么拒绝概率就是  ，或者说接受概率是，这样最后被接受的样本，就会符合  的分布。（PS：严格来说因为被放大了k倍，放大了倍，都已经不是概率函数了，因为积分不为1）

拒绝采样的一个问题是，如果拒绝率很高，则采样的效率很低。因此proposal distribution与目标采样分布越接近越好，这样被拒绝的样本更少。另外如果在高维空间进行采样，则每个纬度上都要被接受，最终样本才能被接受。纬度灾难会让拒绝采样在高维空间的接受率低到不能接受。我们还需要看看有没有更好的算法。

部分现代丈母娘要求的维度越来越多，从文凭到车子房子，从户口到车牌。维度越多，候选码农被拒绝的概率就越大。为了让拒绝率降低一些，码农们只能让自己在这些考核维度的分布，与丈母娘要求的分布越接近越好。但是丈母娘要求的分布也会水涨船高，总是高于码农实现的分布。

2. 重要性采样

重要性采样其实并不是真的采样，或者说可以认为是一种软采样。我们并没有真的拒绝掉或接受一些样本，而是通过把这个样本的权重调低/调高来表达对样本的偏好（拒绝采样中被拒绝的样本可以认为样本权重被置0了）。

现在我们要用从p(x)里采样的样本来计算f(x)的均值，而我们已经实现的是从q(x)中采样（例如q(x)是个高斯分布）。那么我们拆解下f(x)均值计算的公式如下

可以发现，我们只要把从q(x)中采样出来的样本  ，带入到f(x)中，然后用  作为权重，计算加权平均就可以了。扩展一下，如果是希望训练p(x)分布下的模型，但是收集的样本是遵循q(x)分布的时候，也可以用作为样本权重，去训练模型，就一定程度上抹平分布的差异。这也是重要性采样经常被使用的场景。

重要性采样的一个明显的弱点在于，在q(x)=0的地方，因为无法采样到样本，所以即使p(x)在这个地方不为0，也不会采样到样本。对于q(x)很接近0但是略大于0的地方虽然稍微好点，但是由于被采样的概率很低，也需要采样很多的样本才可能采样到这一区间，样本效率很低。因此，和拒绝采样类似，重要性采样也需要proposal distribution与目标分布越接近越好，这样越少的样本就可以得到一个越准确的值。也同样会有在高纬度空间效率指数级下降的问题。不过比拒绝采样好的是，不需要再去寻找让始终在上方的k值了。

乐队的夏天中，超级乐迷有10票，相当于每个人一票，但是权重是10; 专业乐迷，每人两票，相当于权重是2；大众乐迷每人1票，相当于权重是1。这是因为组委会认为，超级乐迷和专业乐迷水平更高，他们的评审水平，更接近于作品的真实水平。

重要性采样的应用领域很广，可以用来解在建模或统计的分布和数据来源分布不一致的问题。例如在强化学习里（例如Youtube那篇年内最大收益的《Top-K Off-Policy Correction for a REINFORCE Recommender System》），因果推断里（用来达到CIA条件做的Propensity Score Weighting，即PSW，其实是目标分布为均匀分布的重要性采样的特例）都经常用到。又是一门算法工程师居家旅行必备技术。

解决了采样的问题，我们来看看怎么在重要性采样里解决的归一化分母不好计算的问题。我们还是用表示没有归一化后的目标“概率密度”函数，用  表示没有归一化后的proposal distribution的“概率密度”函数。把这两个归一化分母提到前面，则有

这里就把计算所需要的分布从p(x)变成了没有归一化的  ，不过我们还需要求出  才行。不过这个值并不难求。

上式的倒数，就是要求的。即对于采样样本  ，计算  的均值，再求一个倒数就可以了。至此，归一化问题也被解决了。

3. MCMC（马尔可夫链蒙特卡洛采样）

接下来要介绍的MCMC的方法，在一些特殊的情况下，可以缓解或解决拒绝采样和重要性采样遇到的高维空间采样效率低的问题，并且同样可以规避的归一化因子难计算的问题。

但是我们需要一点耐心，先从马尔可夫链慢慢聊起。一阶马尔可夫链是指一个序列的随机变量  ，他们满足下面的式子

也就是说，  只和序列里上一个随机变量  有关系，而和之前的其他随机变量（例如  )都没有关系。

马尔可夫链蒙特卡洛采样的基本想法是构造一个特殊的马尔可夫链，使得从这个序列里依次生成出来的值的集合，会遵循我们想要采样的分布。接下来，我们看看如何构造这种特殊的马尔可夫链。在此之前，还有几个概念要先了解下。

（a) 齐次马尔科夫链

如果对于所有的m取值，转移概率  对于任意的取值和的取值，都相同，则我们说这个马尔可夫链是齐次马尔可夫链。也就是说对于任意  ，  (注意这里用加括号表示马尔可夫链中的随机变量，不加表示普通的随机变量)，齐次马尔可夫链都有 

可以理解为在根据每个随机变量的值产生序列里的下一个随机变量的值时，遵循着同样的一个转移概率矩阵，和在序列里的位置无关。

如果我们把转移概率表示为  ，齐次马尔可夫链的转移概率因为对所有m都相同，也就是和m的取值无关，可以计为 ，即 

（b) 概率矩阵，平稳分布与细致平稳条件

如果我们把对应的转移概率放到矩阵  里，使得矩阵里每个元素，则矩阵 就是齐次马尔可夫链的转移概率矩阵。其中表示的是从状态  转移到状态  的概率。

还是刚才的例子，假设随机变量的取值范围是离散的集合  ，我们把当前随机变量x等于不同取值的概率写到一个长度为n向量里。

对于一个以向量表示的分布乘以一个矩阵，即 ，物理意义就是该分布经过一次由矩阵T定义的转移之后，产生的序列里下一个随机变量的概率分布。如果有

也就说下一个随机变量的概率分布和当前一致，没有发生变化。我们说这个分布是关于这个马尔可夫链的平稳分布。回忆一下我们的目标，是要让从马尔可夫链中产生出来的样本服从我们的目标分布，那至少要让这些样本都是从同一个分布中出来的。拆解向量和矩阵乘法的计算规则，会发现下面的式子是p为平稳分布的充要条件

 （式1）

一个充分但是不必要的条件是下面这个式子，这个式子也叫做细致平稳条件（detailed balance）

 （式2）

我们可以证明满足细致平稳条件（式2）的分布，都满足（式1），因此都是平稳分布，证明如下：

（c) 转移矩阵的构造

所以我们现在要做的，就是对于我们想要采样的分布p作为初始分布，构造一个满足上述细致平稳条件的转移矩阵  ，利用这个转移矩阵来生成一系列样本，那么每个样本也会服从这个分布p。

假设我们有一个转移矩阵，但是这个矩阵不符合细致平稳条件，也就是

我们可以通过一个改造来让细致平稳条件得到满足，我们在两边分别乘以  和 

 （式3）

其中

把上式代入（式3）这样等式的两边就完全一样了，自然细致平稳条件也就满足了

也就是说我们新的转移矩阵 需要修改为

我们就得到了一个让细致平稳条件得到满足的转移矩阵。所以我们就可以选择一个我们已经能采样的分布（例如高斯分布）作为  ，然后再以  的概率接受这个采样的结果。如此反复，就能得到一个序列的样本，且样本符合  的分布。看起来胜利就在不远处。

这里还有一个小问题，我们的初始分布一开始并不是符合  的话，那么经过概率转移以后生成的下一个随机变量的分布也不符合。还好如果是齐次马尔可夫链，满足一些很简单的条件(不是本文重点，不增加理解复杂度不展开了，感兴趣的读者google之)，就能成为一个“各态历经”的马尔可夫链。不管初始分布是怎么样的，只要对应的转移矩阵  与某一个分布  满足了细致平稳条件，在经过一定次数的概率转移后（即m趋向于无穷大之后），产生的分布会逼近唯一的平稳分布。

另外一个问题是这里还是有一个的拒绝采样，如果这个值比较小，采样效率还是会比较低。不过有个小trick，可以让这个概率大一些。我们在细致平稳条件的等式两边都乘以同一个数C，等式仍然成立

也就是说我们可以用  代替原来的作为拒绝采样的接受率，我们想办法让尽可能大就好了，但是作为概率值，也不能超过1。也就是说

 且 

所以C最大可以取到

这样，新的接受率

回忆一下，我们还需要考虑的一个问题是分布的归一化分母难计算的问题，这里也刚好就解决了，因为分子分母中都含有归一化分母，自然就约掉了

(d) Metropolis-Hastings算法

到目前为止，我们就得到了一种效率相对比较高的MCMC采样方式，叫做Metropolis-Hastings算法（简写M-H算法）。总结一下M-H算法如下：

1. 选择一个我们已经能采样的分布（例如高斯分布）作为 。(例如  ）
2. 随机获得一个初始样本  ，令 
3. 根据  采样出新的样本  ，以  的概率接受采样出的新样本，如果被拒绝（  的概率），则 。令 
4. 重复3的操作，得到  ，选择  之后的样本（分布收敛到平稳分布之后）作为采样的最终结果。其中M是一个超参数。

如果我们选择的T函数，满足对称性（因为T是我们自己选的，很容易满足），即

则有 

这种特殊的M-H算法，也叫Metropolis Sampling算法。（这个算法在1953年就已经诞生了，而M-H是在1970年在这个基础上进行了通用化）

（e) 吉布斯采样（Gibbs Sampling)

虽然这里  已经被我们专门放大过了，但是在纬度比较高的时候，还是可能会出现接受率比较低的情况。有没有办法把这个接受率始终变成1呢？有的，比如吉布斯采样（Gibbs Sampling）方法。

在后面的推导中，我们需要把随机变量的每一维区分出来，有如下表示方法

其中  表示随机变量 的第1个纬度，表示的除了第k维的其他纬度。

吉布斯采样是M-H采样的一个特例。这里我们先给出吉布斯采样的转移矩阵  ，再证明利用该转移矩阵，会让接受率为1。如果当前随机变量是  ，马尔可夫链下一个随机变量  的时候，如果随机变量和随机变量  除了第k维，其他纬度都一样，也就是说有 ，则转移概率为目标分布  的条件概率分布  。对于不满足这个条件的  ，转移矩阵为0。

同理有

接下来，我们来证明按上面这个转移矩阵采样样本后，接受率为1。回顾一下M-H中的接受率公式，再根据概率公式展开下有

因为需要被判断接受与否的样本，都是从上述的特殊的  中采样出来的，都会满足 （否则转移概率是0，不会被采样出来），所以有  ，  ，代入则有

同理，采样出的样本都会满足  ，代入得到

所以只要按上述的转移矩阵  来采样，接受率是100%。这里又还有一个小问题没解决，即k值是怎么得到的？假设纬度为n，则k是从1到n中随机得到的。严谨一些的话，需要把k值产生的概率，也加到  里，在上面接受率的证明里，很快就会被消元，不影响结论。不过在实际应用的时候，会让k从1到n轮流取得，方便实现。

美中不足的是，在普通的M-H里，我们可以任意选择可采样的分布（例如高斯分布）作为  ，在吉布斯采样中不行了，采样分布必须和目标分布挂钩。

总结一下吉布斯采样（Gibbs Sampling)算法如下：

1. 根据我们的目标分布  ，得到每个纬度的条件分布 
2. 随机获得一个初始样本  ，初始化k=1，m=1
3. 根据每个纬度的条件分布  采样得到  中第k个纬度的值  ，对于其他纬度则直接复制  的值，即 ，这样得到 
4. k=k+1，如果k>n，则重置k=1；m=m+1
5. 重复3，4的操作，得到  ，选择  之后的样本（分布收敛到平稳分布之后）作为采样的最终结果。其中M是一个超参数。

要从的每个纬度（  ）的条件分布中采样也很不容易。在一些具体应用的时候，通常借助有向概率图（也叫贝叶斯网络，注意不是贝叶斯神经网络）或无向概率图（也叫马尔可夫随机场）的工具来去掉一些条件依赖，以及巧妙地选择共轭先后验分布，来解决这个问题。例如经典的用吉布斯采样解LDA，吉布斯采样解受限玻尔兹曼机（RBM）的例子。有兴趣的同学可以自行再深入了解下。

所以，如果不对的分布做任何限制，M-H的采样方法是更通用地从采样的方法。不过缺点就是会有高维空间采样效率较低的问题。所以下面的代码以M-H采样为例（其实是M-H的特例Metropolis Sampling）。

M-H采样训练贝叶斯神经网络的代码样例：

（说明：样例代码的原则是能说明算法原理，追求可读性，所以不会考虑可扩展性，性能等因素。为了兼容用pytorch丹炉的朋友，训练方式用和pytorch更类似的接口。运行环境为python 3，tf 2.3）

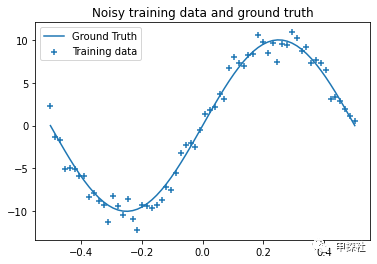
1. 构造一些样本，用来后面训练和展现效果。（此处参考了这篇文章中的样本产生和部分代码，链接：krasserm.github.io/2019）

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

def f(x, sigma):
return 10 * np.sin(2 * np.pi * (x)) + np.random.randn(*x.shape) * sigma

num_of_samples = 64 # 样本数
noise = 1.0 # 噪音规模

X = np.linspace(-0.5, 0.5, num_of_samples).reshape(-1, 1)
y_label = f(X, sigma=noise) # 样本的label
y_truth = f(X, sigma=0.0) # 样本的真实值

plt.scatter(X, y_label, marker='+', label='Training data')
plt.plot(X, y_truth, label='Ground Truth')
plt.title('Noisy training data and ground truth')
plt.legend();

2. 画出的图中，实线是y值的真实分布，“+”号是加上一定噪音后，我们观测得到的样本，也是后面训练用的样本。

3. 先验分布选择了一个由两个高斯分布组成的混合高斯分布

 ，

转移矩阵T选择的是高斯分布  ，可以发现这个分布对于交换i和j后，值不变，也就是对称的。消去接受率公式分子和分母中的 T项，所以有接受率  ，即为M-H的特例：Metropolis Sampling。

from tensorflow.keras.activations import tanh
import tensorflow as tf

class BNN_MH():

def __init__(self, prior_sigma_1=1.5, prior_sigma_2=0.1, prior_pi=0.5):
# 先验分布假设的各种参数
self.prior_sigma_1 = prior_sigma_1
self.prior_sigma_2 = prior_sigma_2
self.prior_pi_1 = prior_pi
self.prior_pi_2 = 1.0 - prior_pi

# 模型中的所有参数，即theta=(w0,b0,w1,b1,w2,b2)
    w0, b0 = self.init_weights([1, 5])
    w1, b1 = self.init_weights([5, 10])
    w2, b2 = self.init_weights([10, 1])
self.w_list = [w0, w1, w2]
self.b_list = [w0, b1, b2]

def init_weights(self, shape):
    w = tf.Variable(tf.random.truncated_normal(shape, mean=0., stddev=1.))
    b = tf.Variable(tf.random.truncated_normal(shape[1:], mean=0., stddev=1.))
return w, b

def forward(self, X, w_list, b_list):
# 简单的3层神经网络结构
    x = tanh(tf.matmul(X, w_list[0]) + b_list[0])
    x = tanh(tf.matmul(x, w_list[1]) + b_list[1])
return tf.matmul(x, w_list[2]) + b_list[2]

def generate_weights_by_gaussian_random_walk(self, step_size = 0.1):
# 高斯随机游走，即从T（x^i -> x^j）= Gaussian(x^i - x^j|0,1.0)中根据已知x^i采样x^j
    next_w0 = self.w_list[0] + tf.random.normal(self.w_list[0].shape)*step_size
    next_b0 = self.b_list[0] + tf.random.normal(self.b_list[0].shape)*step_size
    next_w1 = self.w_list[1] + tf.random.normal(self.w_list[1].shape)*step_size
    next_b1 = self.b_list[1] + tf.random.normal(self.b_list[1].shape)*step_size
    next_w2 = self.w_list[2] + tf.random.normal(self.w_list[2].shape)*step_size
    next_b2 = self.b_list[2] + tf.random.normal(self.b_list[2].shape)*step_size

# 存储x^j
self.next_w_list = [next_w0, next_w1, next_w2]
self.next_b_list = [next_b0, next_b1, next_b2]   

def prior(self, w):
# 先验分布假设
return self.prior_pi_1 * self.gaussian_pdf(w, 0.0, self.prior_sigma_1) \
+ self.prior_pi_2 * self.gaussian_pdf(w, 0.0, self.prior_sigma_2)

def gaussian_pdf(self, x, mu, sigma):
return tf.compat.v1.distributions.Normal(mu,sigma).prob(x)    

def accept_rate(self, X, y_label):   

# 计算先验分布的比率
    prior_ratio = 1.0
for w, w_next, b, b_next in zip(self.w_list, self.next_w_list, \
self.b_list, self.next_b_list):                            
        p_theta = self.prior(w)*self.prior(b)
        p_theta_next = self.prior(w_next)*self.prior(b_next)
        prior_ratio *= tf.reduce_prod(tf.divide(p_theta_next,p_theta))

# 计算似然率的比率
    y_pred = self.forward(X, self.w_list, self.b_list)
    p_d_theta = self.gaussian_pdf(y_label, y_pred, 1.0)
    y_pred_next = self.forward(X, self.next_w_list, self.next_b_list)
    p_d_theta_next = self.gaussian_pdf(y_label, y_pred_next, 1.0) 

    likelihood_ratio = tf.reduce_prod(tf.divide(p_d_theta_next,p_d_theta))

# 接受率等于先验分布的比率*似然率的比率
    ac_rate = prior_ratio * likelihood_ratio
return min(ac_rate,1.0)

def train(self, X, y_label):
self.saved_weights = [] # 存所有w和b值的地方
self.ac_rates = [] # 保存接受率，监控用
    num_of_rounds = 10000
    burn_in_rounds = 1000
for i in range(0,num_of_rounds):
self.generate_weights_by_gaussian_random_walk()
        ac_rate = self.accept_rate(X, y_label)
self.ac_rates.append(ac_rate)
if tf.random.uniform([1]) < ac_rate:
self.w_list = self.next_w_list
self.b_list = self.next_b_list
if i >= burn_in_rounds:
self.saved_weights.append({"w_list":self.w_list, "b_list":self.b_list})
return self.ac_rates

def predict(self, X):
# 用所有存储的参数，分别都预估下模型的输出值
return list(map(lambda saved_weight : self.forward(X, saved_weight["w_list"], \
                                    saved_weight["b_list"]), self.saved_weights))

X = X.astype('float32')
y_label = y_label.astype('float32')

model = BNN_MH()
ac_rates = model.train(X,y_label)
plt.plot(ac_rates)
plt.grid()
X_test = np.linspace(-1., 1., num_of_samples * 2).reshape(-1, 1).astype('float32')
y_preds = model.predict(X_test)
y_preds = np.concatenate(y_preds, axis=1)

plt.scatter(X, y_label, marker='+', label='Training data')
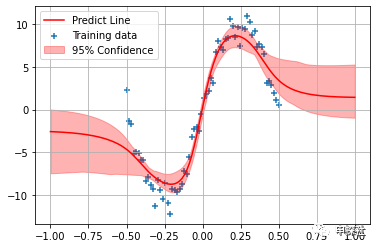
plt.plot(X_test, np.mean(y_preds, axis=1), 'r-', label='Predict Line')
plt.fill_between(X_test.reshape(-1), np.percentile(y_preds, 2.5, axis=1), np.percentile(y_preds, 97.5, axis=1), color='r', alpha=0.3, label='95% Confidence')
plt.grid()
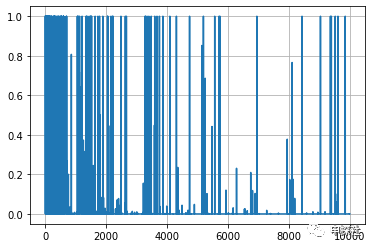
plt.legend()

4. 画出来的曲线是每一轮的接受率

5. 预估阶段，我们把预估的均值和不确定度都画出来

X_test = np.linspace(-1., 1., num_of_samples * 2).reshape(-1, 1).astype('float32')
y_preds = model.predict(X_test)
y_preds = np.concatenate(y_preds, axis=1)

plt.scatter(X, y_label, marker='+', label='Training data')
plt.plot(X_test, np.mean(y_preds, axis=1), 'r-', label='Predict Line')
plt.fill_between(X_test.reshape(-1), np.percentile(y_preds, 2.5, axis=1), np.percentile(y_preds, 97.5, axis=1), color='r', alpha=0.3, label='95% Confidence')
plt.grid()
plt.legend()

6. 图中，红色线条就是所有BNN输出值的均值，也就作为最终的预估值。而红色的区域宽窄，则反应了所有BNN输出值的不确定度（为了方便可视化这里用分位数）。可以看到，对于没有样本的区域，不确定度较大，而对于样本比较密集的地方，不确定度小。另外，在样本有覆盖的领域，转弯的地方，因为要偏离原来的路线，不确定度大；而直线的地方，则不确定度更小。

在（下）篇中，我们会介绍另外一种贝叶斯推断的近似解法，变分推断。也会介绍一种实用的BNN实现MC Dropout，以及讨论实际应用中的一些问题。

还是广告

又到了招聘旺季，我们正在大力寻找志同道合的朋友一起在某手商业化做最有趣最前沿的广告算法，初中高级广告算法职位均有HC（迅速上车，还能赶上上市）。感兴趣的朋友欢迎加我的个人微信约饭约咖啡索要JD或发送简历。（产品和运营也在招人，看机会的朋友我可以帮忙直接推荐给leader们。）

作者个人微信（添加注明申探社读者及简单介绍）：

欢迎扫描下面二维码关注本公众号，也欢迎关注知乎“申探社”专栏