在(上)篇中,我们讨论了什么是不确定度,为什么需要关注不确定度建模,以及不确定度可以怎么用。也从最大似然估计(MLE)到最大后验概率(MAP),讲到了贝叶斯推断(Bayesian Inference)。而我们希望用来建模不确定度的目标模型是贝叶斯神经网络(BNN),它是一种用神经网络来建模似然率,然后进行贝叶斯推断的方法。(中)篇介绍了如何用蒙特卡洛采样的方法来进行贝叶斯推断。而本篇会介绍另外一种方法:变分推断。此外会讲解一个非常容易实现的变分推断特例:MC Dropout。也会讨论在实际应用贝叶斯神经网络(BNN)中的一些问题。本篇涉及内容主要是概念图中的这一部分:
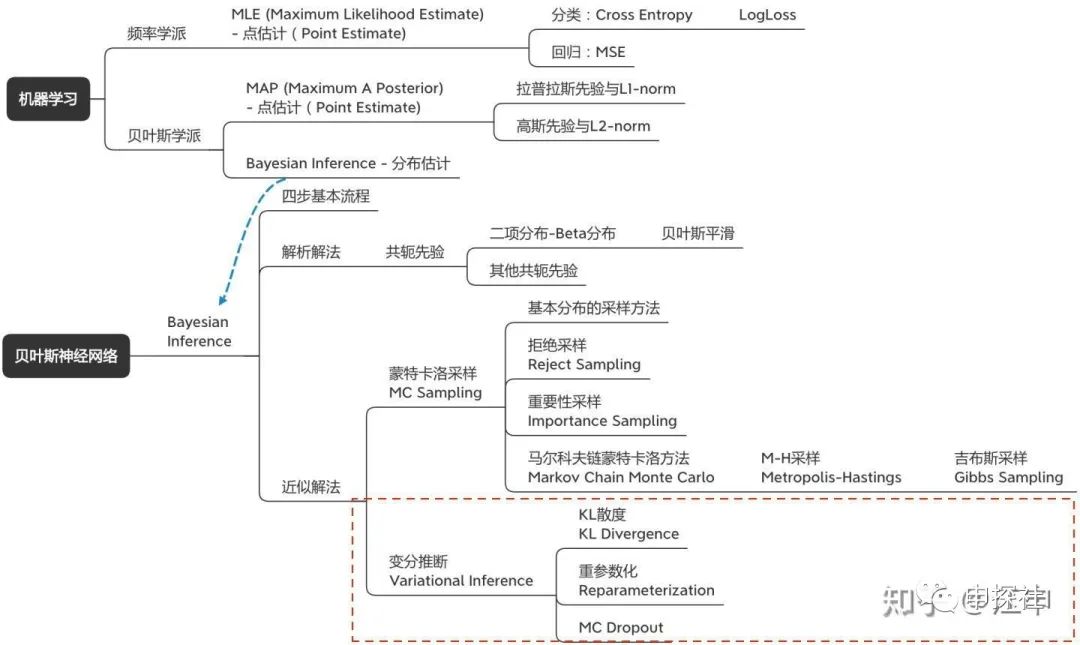
一. 变分推断基本思想
回顾一下,在贝叶斯推断中,我们主要的一个目标是要计算后验概率










明星模仿者,通过不断修正自己的发型,脸型,口音等等参数,使得自己和明星的差距越来越小,最终就可以作为明星的“近似解”去上综艺,做节目了。

这样,我们的目标就变为找到让





根据贝叶斯公式
带入上式可以得到
根据期望值的计算公式 
如果我们引入一个专门的名称ELBO,它等于(注意前面有个负号)
则可以把优化目标写成
因为 


所以我们的Loss就等于-ELBO就好了。不过ELBO里是三个期望值,而 
其中 

Notes 1:我们可以变换下ELBO的表达式,方便我们看看这个表达式内在的含义。
可以发现后面那一项其实就是对数似然率,越大越好。前面那一项则是q分布和先验分布的KL散度,希望q分布和先验分布越近越好。似然率+先验约束,我们的老朋友。
Notes 2: 回忆一下上面的公式
变换下等式,有
因为,所以有
回忆一下,在贝叶斯公式里,p(D)这一项叫evidence,而ELBO是p(D)取值的下界。这也是为什么叫ELBO(Evidence Lower Bound)的原因,
二. 用变分推断训练贝叶斯神经网络
有了可计算的Loss,我们的建模方法很明确了:我们需要建一个神经网络,它的可学习参数是 







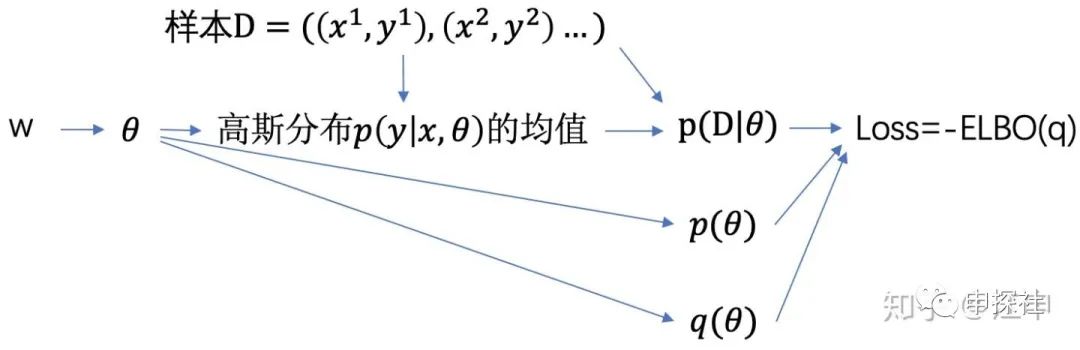
其中网络中从 




那么 



我们把高斯分布做一个变换:
这样我们只需要从 




训练这个神经网络,我们就可以得到最好的 




第一步:假设先验,对似然率建模
第二步:计算后验
展开后有
第三步:计算预测值的分布
第四步:计算y的期望值;
如果需要,计算y的方差作为预估值的不确定度
我们完成了第二步,对于第三步和第四步,我们需要再次借助蒙特卡洛采样的方法(不愧是二十世纪十大算法之一)。从

三. 变分推断的代码示例
(说明:样例代码的原则是能说明算法原理,追求可读性,所以不会考虑可扩展性,性能等因素。为了兼容用pytorch丹炉的朋友,训练方式用和pytorch更类似的接口。运行环境为python 3,tf 2.3)
1. 构造一些样本,用来后面训练和展现效果。(此处参考了两篇文章中的样本产生和部分代码,链接:krasserm.github.io/2019 及zhuanlan.zhihu.com/p/10)
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
def f(x, sigma):
return 10 * np.sin(2 * np.pi * (x)) + np.random.randn(*x.shape) * sigma
num_of_samples = 64 # 样本数
noise = 1.0 # 噪音规模
X = np.linspace(-0.5, 0.5, num_of_samples).reshape(-1, 1)
y_label = f(X, sigma=noise) # 样本的label
y_truth = f(X, sigma=0.0) # 样本的真实值
plt.scatter(X, y_label, marker='+', label='Training data')
plt.plot(X, y_truth, label='Ground Truth')
plt.title('Noisy training data and ground truth')
plt.legend();
2. 画出的图中,实线是y值的真实分布,“+”号是加上一定噪音后,我们观测得到的样本,也是后面训练用的样本。

3. 与(中)篇的蒙特卡洛法一样,先验分布选择了一个由两个高斯分布组成的混合高斯分布
不出意外 

其中
这里对高斯分布的方差做了一些小设计,据说可以帮助 
from tensorflow.keras.activations import relu
from tensorflow.keras.optimizers import Adam
import tensorflow as tf
class BNN_VI():
def __init__(self, prior_sigma_1=1.5, prior_sigma_2=0.1, prior_pi=0.5):
# 先验分布假设的各种参数
self.prior_sigma_1 = prior_sigma_1
self.prior_sigma_2 = prior_sigma_2
self.prior_pi_1 = prior_pi
self.prior_pi_2 = 1.0 - prior_pi
# (w0_mu,w0_rho)是用来采样w0的高斯分布的参数,其他类似
self.w0_mu, self.b0_mu, self.w0_rho, self.b0_rho = self.init_weights([1, 5])
self.w1_mu, self.b1_mu, self.w1_rho, self.b1_rho = self.init_weights([5, 10])
self.w2_mu, self.b2_mu, self.w2_rho, self.b2_rho = self.init_weights([10, 1])
# 把所有的mu和rho放在一起好管理,模型里可学习参数是mu和rho,不是w和b
self.mu_list = [self.w0_mu, self.b0_mu, self.w1_mu, self.b1_mu, self.w2_mu, self.b2_mu]
self.rho_list = [self.w0_rho, self.b0_rho, self.w1_rho, self.b1_rho, self.w2_rho, self.b2_rho]
self.trainables = self.mu_list + self.rho_list
self.optimizer = Adam(0.08)
def init_weights(self, shape):
# 初始化可学习参数mu和rho们
w_mu = tf.Variable(tf.random.truncated_normal(shape, mean=0., stddev=1.))
b_mu = tf.Variable(tf.random.truncated_normal(shape[1:], mean=0., stddev=1.))
w_rho = tf.Variable(tf.zeros(shape))
b_rho = tf.Variable(tf.zeros(shape[1:]))
return w_mu, b_mu, w_rho, b_rho
def sample_w_b(self):
# 根据mu和rho们,采样得到w和b们
self.w0 = self.w0_mu + tf.math.softplus(self.w0_rho) * tf.random.normal(self.w0_mu.shape)
self.b0 = self.b0_mu + tf.math.softplus(self.b0_rho) * tf.random.normal(self.b0_mu.shape)
self.w1 = self.w1_mu + tf.math.softplus(self.w1_rho) * tf.random.normal(self.w1_mu.shape)
self.b1 = self.b1_mu + tf.math.softplus(self.b1_rho) * tf.random.normal(self.b1_mu.shape)
self.w2 = self.w2_mu + tf.math.softplus(self.w2_rho) * tf.random.normal(self.w2_mu.shape)
self.b2 = self.b2_mu + tf.math.softplus(self.b2_rho) * tf.random.normal(self.b2_mu.shape)
self.w_b_list = [self.w0, self.b0, self.w1, self.b1, self.w2, self.b2]
def forward(self, X):
self.sample_w_b()
# 简单的3层神经网络结构
x = relu(tf.matmul(X, self.w0) + self.b0)
x = relu(tf.matmul(x, self.w1) + self.b1)
self.y_pred = tf.matmul(x, self.w2) + self.b2
return self.y_pred
def prior(self, w):
# 先验分布假设
return self.prior_pi_1 * self.gaussian_pdf(w, 0.0, self.prior_sigma_1) \
+ self.prior_pi_2 * self.gaussian_pdf(w, 0.0, self.prior_sigma_2)
def gaussian_pdf(self, x, mu, sigma):
return tf.compat.v1.distributions.Normal(mu,sigma).prob(x)
def get_loss(self, y_label):
self.loss = []
for (w_or_b, mu, rho) in zip(self.w_b_list, self.mu_list, self.rho_list):
# 这里的q_theta_w和文章对应,其中的w指的是(mu,rho), 而w_or_b中的w就是权重中的w
q_theta_w = tf.math.log(self.gaussian_pdf(w_or_b, mu, tf.math.softplus(rho)) + 1E-30)
p_theta = tf.math.log(self.prior(w_or_b) + 1E-30)
# 公式中三项中的两项
self.loss.append(tf.math.reduce_sum(q_theta_w - p_theta))
p_d_theta = tf.math.reduce_sum(tf.math.log(self.gaussian_pdf(y_label, self.y_pred, 1.0) + 1E-30))
# 公式中三项中的另外一项
self.loss.append(tf.math.reduce_sum(-p_d_theta))
return tf.reduce_sum(self.loss)
def train(self, X, y_label):
loss_list = []
for _ in range(2000):
with tf.GradientTape() as g:
self.forward(X)
loss = self.get_loss(y_label)
gradients = g.gradient(loss, self.trainables)
self.optimizer.apply_gradients(zip(gradients, self.trainables))
loss_list.append(loss.numpy())
return loss_list
def predict(self, X):
return [self.forward(X) for _ in range(300)]
X = X.astype('float32')
y_label = y_label.astype('float32')
model = BNN_VI()
loss_list = model.train(X,y_label)
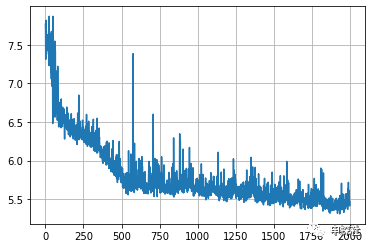
plt.plot(np.log(loss_list))
plt.grid()
4. 画出来的曲线是每一轮的loss
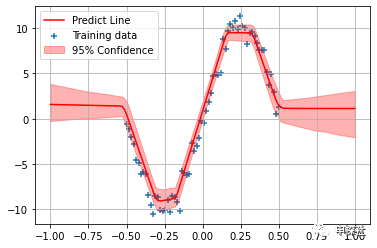
5. 预估阶段,我们把预估的均值和不确定度都画出来
X_test = np.linspace(-1., 1., num_of_samples * 2).reshape(-1, 1).astype('float32')
y_preds = model.predict(X_test)
y_preds = np.concatenate(y_preds, axis=1)
plt.scatter(X, y_label, marker='+', label='Training data')
plt.plot(X_test, np.mean(y_preds, axis=1), 'r-', label='Predict Line')
plt.fill_between(X_test.reshape(-1), np.percentile(y_preds, 2.5, axis=1), np.percentile(y_preds, 97.5, axis=1), color='r', alpha=0.3, label='95% Confidence')
plt.grid()
plt.legend()
6. 图中,红色线条就是所有BNN输出值的均值,也就作为最终的预估值。而红色的区域宽窄,则反应了所有BNN输出值的不确定度(为了方便可视化这里用分位数)。可以看到,结果和(中)篇中蒙特卡洛采样法得到的结果是类似的:对于没有样本的区域,不确定度较大,而对于样本比较密集的地方,不确定度小。另外,在样本有覆盖的领域,转弯的地方,因为要偏离原来的路线,不确定度大;而直线的地方,则不确定度更小。
四. MC Dropout
前面介绍的蒙特卡洛采样法和变分推断的方法,实现起来都略显复杂。对比之下,接下来介绍的这个方法,实现非常简单,适合工业界应用。
这个方法的做法简单到只有两句话:在原有的只预估均值的神经网络里,为每一层的所有权重都添加Dropout层,然后在预估(inference)的时候,让dropout继续生效。这样同一个样本,每次inference都会预估出不一样的值(因为有dropout),把这些值的均值,就作为预估值,这些值的方差,就作为预估值的不确定度。(Paper链接:proceedings.mlr.press/v)
这个做法,可以证明效果和变分推断是等效的。不过尽管做法这么简单,但是这个证明却非常复杂,感兴趣的朋友可以看这个证明文档(文档链接:arxiv.org/pdf/1506.0215)
MC Dropout就像在巨无霸汉堡的每一层肉中间,都加上一层生菜。

我们介绍的训练贝叶斯神经网络的三种方法的异同如下

对于MC Dropout来说,也可以认为在Inference阶段, 

其中 
其中k为dropout的保留率。
因此MC Dropout作为一种变分推断的一个特例,在这一点上是一致的,

五. MC Dropout代码示例
1.(这里略去了生产样本的代码,和上面普通变分推断的代码是精确一致的)我们直接用keras的接口,像普通神经网络一样把结构搭建起来,唯一的不同是每层之间都插入了Dropout层。
import tensorflow as tf
from tensorflow.keras.optimizers import Adam
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(1,1)),
tf.keras.layers.Dense(30, activation='tanh'),
tf.keras.layers.Dropout(0.3),
tf.keras.layers.Dense(30, activation='tanh'),
tf.keras.layers.Dropout(0.3),
tf.keras.layers.Dense(1, activation='linear')
])
model.compile(optimizer=Adam(learning_rate=0.1),
loss='mean_squared_error',
metrics=['MeanSquaredError'])
model.fit(X, y_label, epochs=2000)
2. 在预测的时候,通过 training=True 这个设置,使得Dropout层在inference的时候,也会概率丢弃一部分节点。不设置这个参数的话,dropout层在inference的时候,默认是会保留所有的节点,不执行dropout。
X_test = np.linspace(-1., 1., num_of_samples * 2).reshape(-1, 1).astype('float32')
y_preds = [model(X_test, training=True) for _ in range(300)]
y_preds = np.concatenate(y_preds, axis=1)
plt.scatter(X, y_label, marker='+', label='Training data')
plt.plot(X_test, np.mean(y_preds, axis=1), 'r-', label='Predict Line')
plt.fill_between(X_test.reshape(-1), np.percentile(y_preds, 2.5, axis=1), np.percentile(y_preds, 97.5, axis=1), color='r', alpha=0.3, label='95% Confidence')
plt.grid()
plt.legend()
3. 图中,红色线条就是所有BNN输出值的均值,也就作为最终的预估值。而红色的区域宽窄,则反应了所有BNN输出值的不确定度(为了方便可视化这里用分位数)。可以看到,结果和(中)篇中蒙特卡洛采样法或普通变分推断的结果是一样的。

六. 不确定度建模实际应用中的一些问题
(1) 对现有系统侵入性
不管是蒙特卡洛采样法还是普通的变分推断,对原有的CXR模型来说,都需要对模型结构或者训练流程做较大的改动。这也是阻拦不确定性建模落地的主要原因。而MC Dropout对原有模型的侵入型很小,比较方便落地。对于添加的dropout层,也许本来也可以帮助模型抑制过拟合,而提高预估的准确性。
(2) 性能问题
相比普通的模型,贝叶斯神经网络要预估出很多个值,再求方差来作为不确定度的度量,在线inference时的计算量会翻几倍,对性能会有较大影响。可以考虑做以下几点的优化来缓解性能问题:
1. 只在最顶上几层添加dropout做tradeoff。虽然理论上不能保证和变分完全等效,但是在笔者的实验中,效果也是可接受的。
2. 原有模型不变,仍旧只预估期望值。单独使用一个结构更简单的模型,再加上dropout来预估不确定度。可以这么做是因为不确定度的精度不需要那么高。另外这样的好处是可以完全和原有模型结耦,0侵入性。但是缺点是这个更简单的模型,和原有模型不一致,不确定度和预估值不是一起训练出来的,可能会“不配套”。
3. 在线inference时每次inference是独立的,可以进行并行化。对于变分推断(包括MC Dropout)可以先把 
4. 事实上,在很多实际应用场景,因为对不确定度的预估准确度要求并不高,因此对实时性的要求也不高,我们可以通过离线计算来缓存不确定度,然后定期更新就好。例如我们主要关心新广告的不确定度,则可以定期采样一些涉及该广告的请求,然后离线计算出这些请求的不确定度,再取平均(抹平人群和上下文差异)作为该广告的不确定度。如果需要关心某人群与新广告组合的不确定度,也可以如法炮制,离线统计人群与新广告交叉纬度的平均不确定度。
(3)不确定度的预估准确性评估
贝叶斯神经网络模型中用了不同的网络结构,或者不同的超参数,哪个模型预估的不确定度更准确呢?要直接评估不确定度预估的准确性不太容易,我们只好通过两个间接评估的方法来评估。
直接评估不好评估,则考虑间接评估的例子如下。

方法一:如果我们是通过预估y值的分布,再用方差来作为不确定度的度量,则可以通过评估y值分布的准确性来间接评估方差的准确性。我们先用训练集进行模型训练,然后在测试集上做评估。对有n个样本的测试集中每个样本 




如果我们的任务是regression,如前文所述,神经网络的输出为高斯分布 

测试集的平均log似然率越高,说明预估的y分布,和实际分布越符合。从直觉来看,当对某个样本的y值的预估方差较小时,如果实际的y值方差较大,也就是落在离均值比较远的地方,则会有一个较低的似然率,从而惩罚偏小的预估方差;而当预估方差较大时,如果实际的y值方差较小,即y值都落在均值附近的地方,也会因为均值附近概率密度被分掉一部分到其他地方,而得到一个较低的似然率,从而惩罚偏大的预估方差。
不过平均log似然率评估的是整个分布的预估准确度,也包括了均值的预估准确度。所以log似然率的提升,不一定是不确定度预估准确性的提升。
方法二:直接评估不好评估,我们只好通过使用了不确定度预估值的任务的效果来间接评估了。下面用冷启动作为一个例子,但是其他的任务也都可以设计相应的方法。在冷启动中,我们使用不确定度来决定探索哪些广告,那么我们就可以根据探索的效率来评估不确定度预估的准确度。
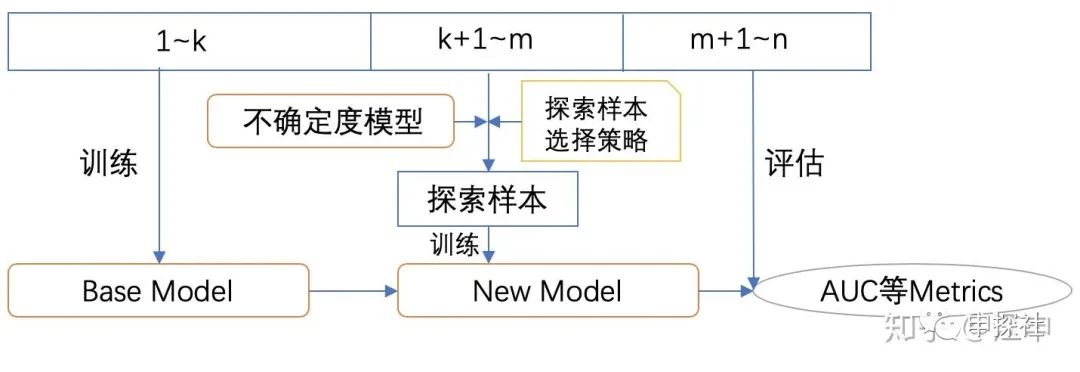
我们可以先用第1到第k天的样本训练一个Base模型 









上面的这个流程的原理,是不是和Meta Learning的有些类似?如果我们把Base模型的模型结构或超参数,不确定度模型的结构或者超参数,以及探索样本选择策略,都作为meta模型的可学习参数,我们就可以试图去学一个好的学习方法,这个学习方法好不好,则可以通过在最终测试集上的AUC等metrics来评估。最终得到一个较好的学习方法,可以在同样的探索成本下,获得最高的模型效果提升,也就是冷启动探索效率的提升。
当然,实际线上的冷启动任务比构造的这个任务要更复杂,例如在这个任务中,通过限制探索样本的数量来限制探索所需要的成本,而实际线上搜集每个样本的成本是不相同的,数量一致不代表资源一致。
讲到这里,本系列的主要内容就介绍完了,感谢大家的支持。希望大家共同来探索不确定度建模在广告系统中的应用。
还是广告
又到了招聘旺季,我们正在大力寻找志同道合的朋友一起在某手商业化做最有趣最前沿的广告算法,初中高级广告算法职位均有HC(迅速上车,还能赶上上市)。感兴趣的朋友欢迎加我的个人微信约饭约咖啡索要JD或发送简历。(产品和运营也在招人,看机会的朋友我可以帮忙直接推荐给leader们。)
作者个人微信(添加注明申探社读者及简单介绍):

欢迎扫描下面二维码关注本公众号,也欢迎关注知乎“申探社”专栏

文章为作者独立观点,不代表DLZ123立场。如有侵权,请联系我们。( 版权为作者所有,如需转载,请联系作者 )

网站运营至今,离不开小伙伴们的支持。 为了给小伙伴们提供一个互相交流的平台和资源的对接,特地开通了独立站交流群。
群里有不少运营大神,不时会分享一些运营技巧,更有一些资源收藏爱好者不时分享一些优质的学习资料。
现在可以扫码进群,备注【加群】。 ( 群完全免费,不广告不卖课!)






























发表评论 取消回复