申探社：不确定度建模（上）- 贝叶斯推断基础

在广告系统中，CTR， CvR等模型想必大家都非常熟悉了。将一个包含一系列特征值的样本输入CTR, CvR模型，模型输出一个点击率或者转化率的预估值。有时候我们也会遇到一些情况，除了需要预估值之外，还需要知道预估值的不确定度（Uncertainty）（或者预估值的分布，有了分布，通常不确定度也能算出来）。

我们从三个问题引出今天的讨论。

问题一: 什么是不确定度？

有些朋友可能对不确定度没有什么概念。举个例子：

广告A: 3个展现1个点击，因此点击率为1/3
广告B: 300个展现100个点击，因此点击率为1/3

这个时候我们对广告A与B的点击率预估值可能都是1/3，但是因为广告A的样本数很少，如果因为一些随机因素少来一个点击或者多来一个点击，点击率都会发生巨大变化，因此广告A点击率为1/3的不确定度要大于广告B。从通俗的语言来理解，“不确定度”就是“预估准不准”的意思。如果点击率模型会说话，它会说：“主人，我会把这两个广告的点击率都预估为1/3，但是我对广告A的预估没什么把握，可能会不准，你要小心使用”。

问题二：为什么要关注不确定度建模？

在广告系统中，对于不确定度的建模，虽然没有CXR建模来说那么关键，但是随着两个趋势的发展，也越来越重要了。第一个趋势是广告主要优化的链路深度越来越深（以前优化到激活就可以，现在要优化到付费，付费金额），而后链路数据越往后越稀疏。广告主的深度链路优化需求，就像-11034米的马里亚纳海沟，我们对它的观测数据非常稀少，那里有什么东西的不确定度非常大。第二个趋势是广告素材逐渐从图文载体向衰减速度更快的短视频载体迁移。广告主必须不断上新素材，新素材占比越来越高。更深的后链路事件，会让CvR的样本更加稀疏；而新素材也就意味着素材的行为数据更加稀少，相关的CXR样本更加稀疏 。这个时候，怎么能通过不确定度来区分对待置信和不置信的预估值，就变得更加重要了。

问题三：不确定度可以怎么用？

不确定度在广告系统中的应用可以大概分为两类：一是在探索与利用（E&E）中，用来更有效率地降低不确定度；二是基于不确定度进行策略决策。

我们先来看第一类应用，在此之前先介绍下不确定度建模的一个最简单的方法：

其中n为包含目标对象（item）的样本数。在实际工作里，很多时候用这个简单的方法来估计不确定度就够了。在很多经典算法里，实时上也是近似地用了这个公式，例如E&E里UCB算法。假设我们要估计刚才那两个广告点击率的不确定度，n就等于每个广告的曝光次数，那么广告A的不确定度为  ，而广告B的不确定度只有，是广告A的十分之一。广告B比广告A曝光增加了100倍，不确定度只变成原来1/10，而不是1/100。所以我们可以发现，随着曝光的增加，不确定的下降速度是慢慢降低的。而最开始的几次曝光，让不确定度下降得最明显。如果我们的目标是让所有广告总的不确定度下降最多的话，那么选已曝光次数少的（也就是不确定度高的，带来信息量大的），是效率比较高的方式。所以很多E&E策略，在探索的时候会根据item不确定度值的高低，来决定item被探索的概率。当然，不确定度只是决定探索概率的一个重要因素，还有很多其他因素也需要考虑，但不是本文重点，不再赘述。

可是这种最简单的不确定建模方式的问题是，完全忽略了item之间的关系。例如广告A和广告B很相似，我们推一下极端，假设它两完全一样：都用了素材A，都推广产品B，定向出价都是一样的。那么如果广告A已经被展现了300次，有100次点击，点击率是1/3。理想情况下，即使广告B完全没有展现，它的点击率预估值的不确定度也应该是和广告A一样的（广告B借用了广告A的展现数据来降低了自己预估值的不确定度）。但是用上面简单的方法，不确定度还是（其中n=0），也就是无穷大。如果广告B只是和广告A用一样的素材，但定向出价是不一样的。那么广告B预估值的不确定度应该是大于广告A的不确定度，但是小于无穷大。所以为了得到更加精细的不确定度，就得考虑有泛化能力的不确定度建模方法，可以把其他相似广告的不确定度泛化到目标广告。这些更复杂的建模方法和的差异大不大呢？基本上可以认为跟用点击率预估模型来预估一个广告的点击率和用这个广告自己的后验数据（点击数/展现数）来预估这个广告点击率的差异差不多。值不值得做，就看具体业务场景的需求了。

如果使用了有泛化能力的不确定建模方法，除了得到一个更准确的不确定度预估值之外，还有一个好处是，我们在选择探索的item的时候，可以主动选择那些可以将不确定度泛化给更多其他item的item来进行探索（例如与很多其他item都相似的item），探索完一个item，可以降低一批item的不确定度，从而提高每次探索能降低的总不确定度。就像农药里蔡文姬的二技能“弹弹弹”，攻击一个敌人，伤害一群敌人。

在广告系统中，除了广告冷启动，还有很多需要做E&E的地方，都可能会用到不确定度，例如其他纬度冷启动（如素材冷启动，用户冷启动），投放系统E&E，模型训练/投放系统的超参数搜索，智能扩量等等。另外，不确定度建模在强化学习里，也有成熟的应用。例如强化学习里agent在一个environment学习，为了提高学习效率，需要尽量走到不确定性高的地方（类似E&E场景），这样能收集到的样本带来的信息量最大。

接下来，我们看看不确定度的第二类应用场景，基于不确定度进行策略决策。

为什么在决策中只考虑预估值不够，也需要考虑不确定度呢？举个例子来说，坐公交车到公司平均需要30分钟，但是可能因为堵车需要40分钟，也可能因为一路绿灯，只需要20分钟。坐地铁也平均需要30分钟，但是几乎不受其他因素影响，非常准时。显而易见，坐公交车上班为30分钟的不确定度要大于坐地铁上班为30分钟的不确定度。如果要上班不迟到，坐公交车就得提早40分钟出门，而坐地铁只需要提早30分钟。这就是决策不能只考虑期望值，也得考虑不确定度的一个例子。

对于广告来说，以刚才的例子来说，广告B的点击率为1/3已经很确定了，如果成本是达标的，那么投放系统就可以大胆放量了。对于广告A的点击率为1/3，是还不太确定的，可能更高，可能更低。为了不要超成本，广告系统的一个可能更优的选择是通过出比广告B稍微低一些的价格保守投放广告A，等到积累的展现点击数更多了，再大胆投放。在广告系统中，智能出价，智能定向等等产品中都可能会用到不确定度进行策略决策。

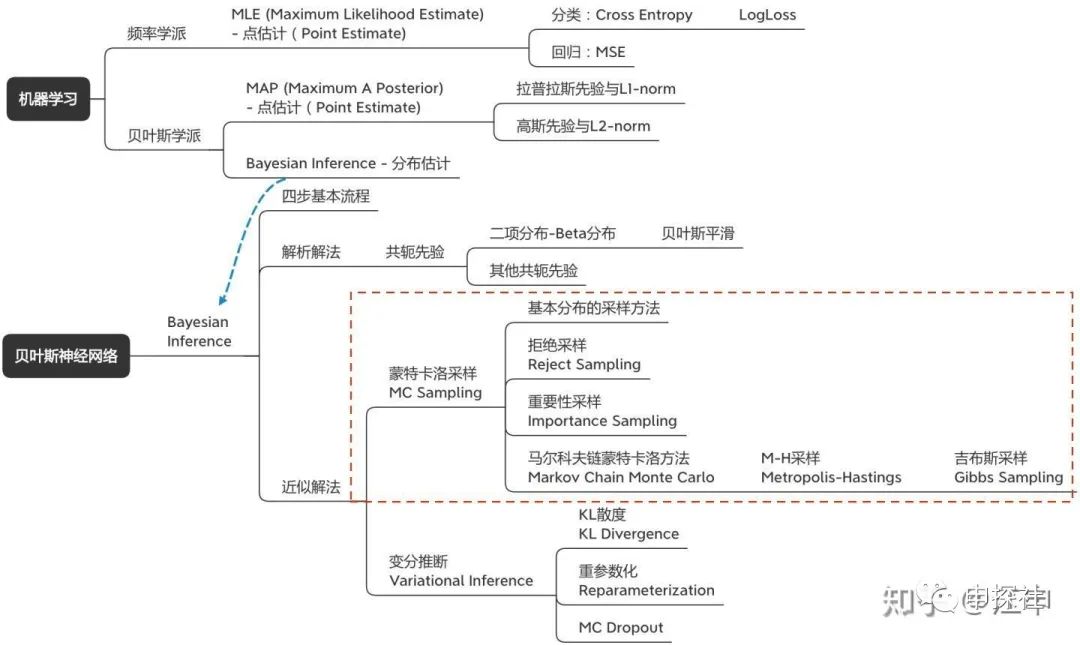
本文最终要介绍的贝叶斯神经网络（BNN）是一种用神经网络（当然也可以不用神经网络，只是那样文章估计没人要看）来建模不确定度的模型，这个模型的输入和普通模型一样，但是输出的是一个预估值的分布而不是单独的一个预估值。有了这个预估值的分布，我们也可以再算出分布的期望值作为最终预估值，也可以得到这个分布的方差来表征的不确定度。预估出来的是分布，网络中的权重也是分布（在具体实现的时候，权重和预估值的分布，大多数是通过从分布中采样的样本集来近似表示）。

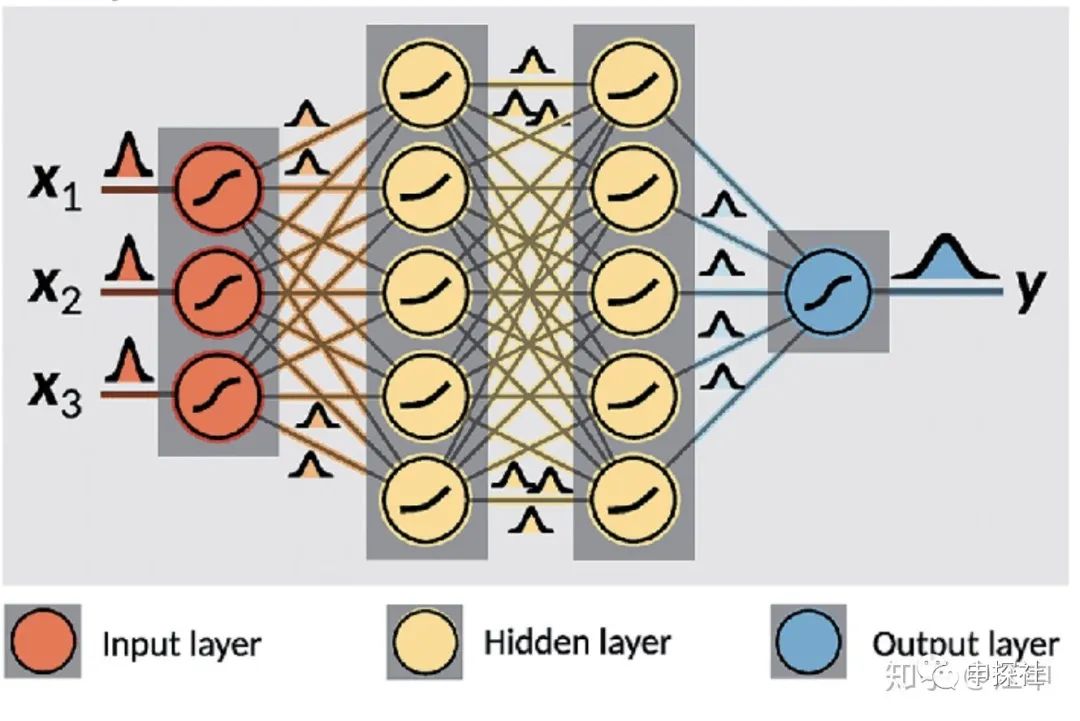
（图片来源链接：https://www.researchgate.net/publication/329843608_How_machine_learning_can_assist_the_interpretation_of_ab_initio_molecular_dynamics_simulations_and_conceptual_understanding_of_chemistry）

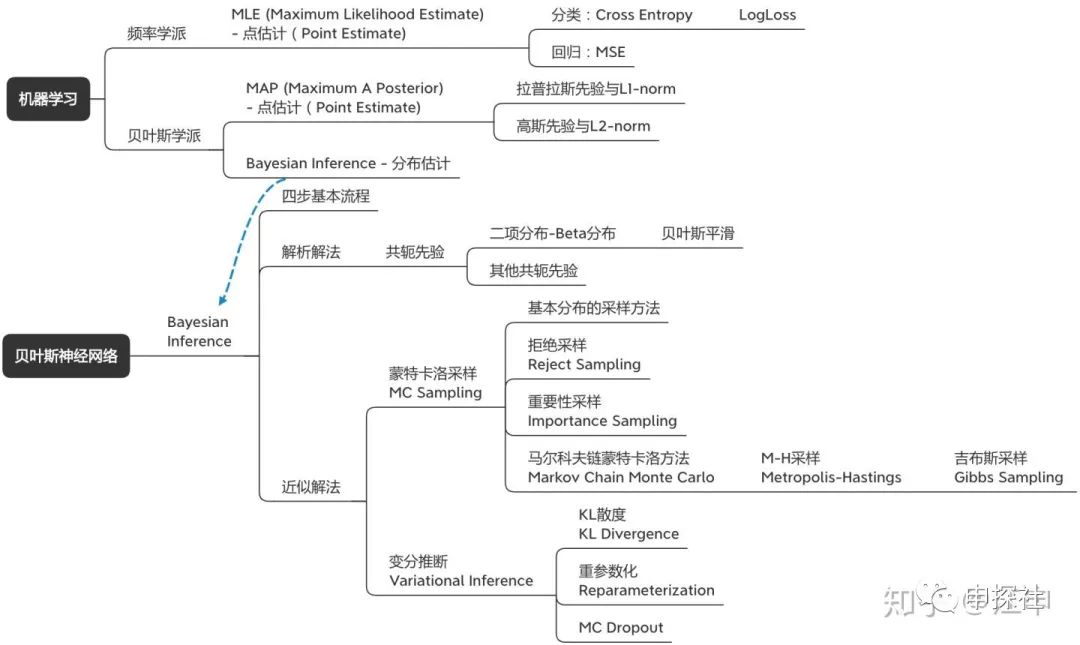
贝叶斯神经网络涉及到的概念树大概长下面这个样子。里面有很多概念其实每一个单独自身也是非常有意思的话题。我自己觉得这篇文章可能一方面是希望把贝叶斯神经网络讲明白，而逐渐把涉及的概念讲清楚；从另外一个角度来说，也是想把这些有意思的概念通过一个结构给串起来（乔布斯的connecting the dots)。因为只有成结构的知识体系，才比较容易被理解和记忆。为了保证大家理解的顺畅度，本文尽量保证全文用统一的一套数学标记和符号，因此公式全部重新手打，难免有错误的地方，欢迎大家指出。

废话不多说，我们的旅程从经典的贝叶斯公式开始：

（对于没有见过这个公式的朋友，可能本系列的文章读起来会有些吃力了。）

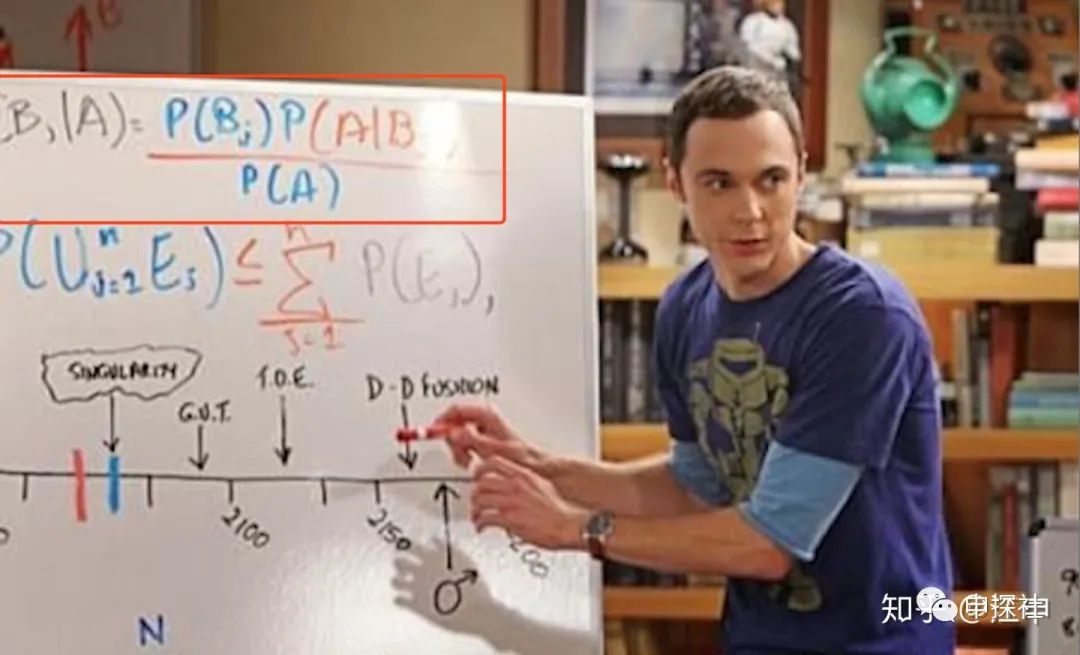
这个公式里，D是观察数据或者是训练的样本，  是模型的参数。  叫似然率（Likelihood)，  叫先验(Prior)，  叫后验(Posterior)，  叫证据（Evidence)。

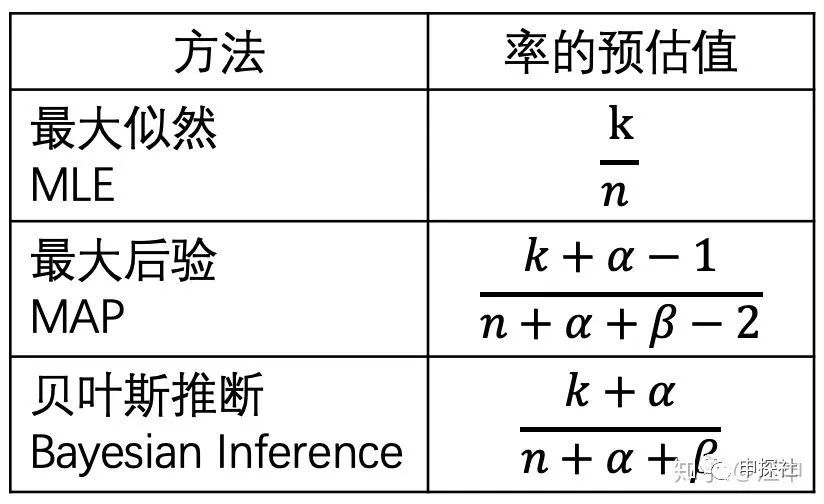
很多的资料上有所谓频率学派与贝叶斯学派之分，但其实现在很少有人会区分这两者。通常来说，频率学派从最大似然率的角度来训练模型(MLE)，而贝叶斯学派通常用两种方法，一种是最大后验概率(MAP)，另外一种是贝叶斯推断（Bayesian Inference)。

一. 最大似然估计（MLE）

大家平时经常使用的几种Loss，例如交叉熵，LogLoss，MSE（Mean Square Error）其实都是某种分布假设下的MLE。也就是说，大多数时候，大家通常是站在频率学派的角度。接下来我们通过公式推导来展现他们之间的关系。对推公式不感兴趣的读者，也可以跳过证明的部分，记得黑体字的结论就可以了。

1. 最小化交叉熵=最小化KL散度=最大似然估计（MLE）

其中  (简写为P)就是真实值的分布，  (简写为Q)是预估模型预估值的分布，  就是P分布和Q分布的交叉熵。如下面的公式，根据交叉熵的定义，可以把H(P,Q)展开为P的熵H(P)和P到Q的KL散度  之和。因为H(P)即真实分布的熵与  无关（  是个常数），因此最小化他们的交叉熵，就等于最小化P到Q的KL散度。

我们把P和Q的简写展开，再把KL的定义带入，则有

这里需要回顾一下微积分公式  ，当x的分布是p(x)时，这个积分求出来的就是f(x)的均值。所以有

我们的训练样本  就是从真实样本中采样得到的，因此有

同样的，  与  无关，所以可以从argmin里去掉，则有

上式就是最大似然估计，得证！

2. Log Loss是在二分类情况下的交叉熵（Cross Entropy)

对于比如点击率预估来说，P和Q都服从伯努利分布。也就是说

 ，

则

上式也叫做Log Loss，即Log Loss是在二分类情况下的交叉熵（Cross Entropy)。因此最小化Log Loss本质上也是最大似然估计（MLE）

3. 如果我们用正态分布来建模预估值，

 ，其中 

那么似然率就是：

最大化上式（即MLE），等于最小化  ，即MSE。

通过上面三个证明，把大家平时用得最多的交叉熵，logloss， MSE作为loss的方法，都归到了MLE的范围内。MLE最大的特点就是不考虑先验分布。接下来我们看看把先验分布纳入会发生什么变化。

二. 最大后验概率（MAP）

接下来我们来讨论最大后验概率MAP（Maximize a Posterior), 所谓后验（Posterior) 即下面这个式子

因为  是与参数  无关的量，因此求argmax的时候可以把P(D)去掉，即：

我们可以看到MAP和MLE的区别，就在于后面乘了一个先验  。这个先验的作用是在训练数据不充分的时候，让参数有一个更加符合先验假设的值，防止参数过拟合。说到防止过拟合，大家可能都会想到最经典的L1-norm和L2-norm。事实上，我们可以证明，如果先验选择协方差矩阵为单位矩阵常数倍的高斯分布，则MAP=MLE+L2-norm，而如果先验选择协方差矩阵为单位矩阵常数倍的拉普拉斯分布，则MAP=MLE+L1-norm。

证明如下：

因为 为协方差矩阵为单位矩阵常数倍的高斯分布，即

展开高斯分布则有

其中 替代了那一堆常数，  也就是L2-norm正则项前面的系数。得证！

同理，如果先验  选择拉普拉斯分布，则有

同样地，展开拉普拉斯分布

其中 替代了那一堆常数，  也就是L1-norm正则项前面的系数。得证！

MAP相比MLE，用先验起到了类似正则项的作用，控制模型不过拟合。MAP的全称是maximium a posteriori, 这里的A表示这只是最大化了其中一个点，有时候这会引发一些问题。举个例子，假设后验分布随着参数  的变化的分布如下图：

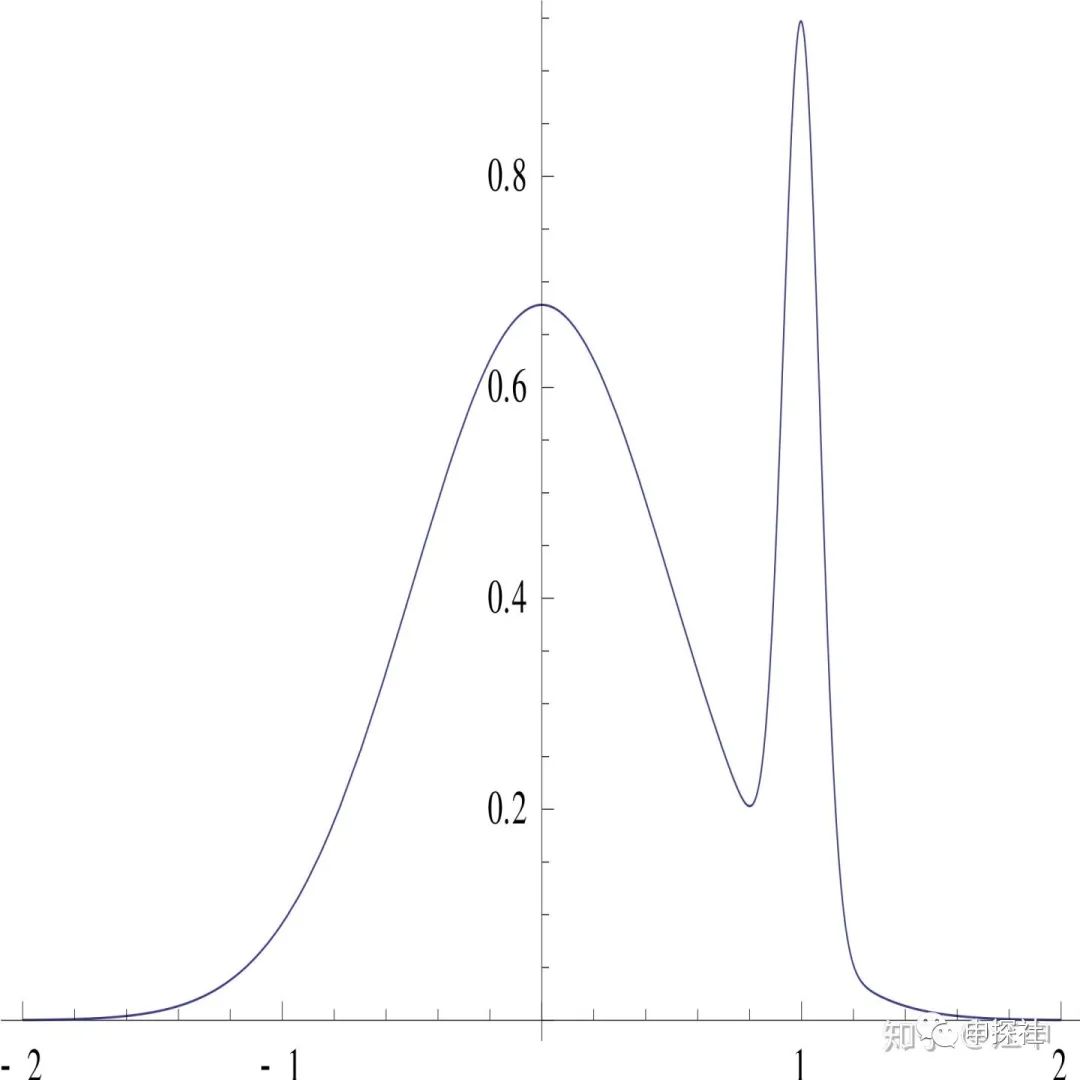
那么如果用MAP选出来的 就会是1，而我们通过观察上图，会发现0其实才是更好的选择。大部分的概率密度是分布在0附近，1其实更像是个异常点。这就是点估计带来的局限性，没有考虑整个分布的形状，只用了1个数来取代了整个分布。如果要考虑整个分布，那么不能只学习一个  , 而是要把  的整个分布学习下来，再用整个的分布去做预估。所以更加理论完美的方式是用贝叶斯推断。

三、贝叶斯推断

贝叶斯推断通常遵循以下的四步：

第一步：假设先验  ，对似然率建模 
第二步：计算后验 
展开后有 
第三步：计算预测值的分布 
第四步：计算y的期望值  ；
如果需要，计算y的方差  作为预估值的不确定度

为了对比，我们把MAP的也列一下：

第一步：假设先验  ，对似然率建模 
第二步：计算让后验 最大的 记为 
第三步：将带入中。对于很多的建模中，都会将均值表示为  的表达式。例如用伯努利分布建模的点击率，  就是均值；再例如用均值和方差参数的高斯分布来建模，均值也是  或者  的表达式，带入就可以得到y的均值（期望值）。

对比后可以发现，点估计（MLE或者MAP）相比贝叶斯推断，最主要的区别在于只用了一个点  来代替整个  的分布，这个分布是否分散（不确定度是否高）的信息就被丢掉了。而在贝叶斯推断里，我们可以认为是按照这个分布采样了无数个  ，对每个都计算出对应的，然后再把所有的平均起来，得到最终的，也会比点估计得到的更加的准确。（当然，代价就是计算复杂度要高很多）

如果每个是一个创造营的观众的话，的分布就是观众的分布。点估计就好比在所有观众里，找一个最有代表性的观众，用他对练习生的投票的分布，作为最终练习生的排名。而贝叶斯推断里可以认为每个观众的投票分布是，我们把所有观众的投票汇总，得到最终的总排名分布，要比最有代表性观众的投票更能反映练习生的受欢迎程度。

四、贝叶斯平滑

接下来，我们举个完整的例子，来对比下MLE，MAP和贝叶斯推断。在广告或者推荐里，我们经常需要根据历史展现数n，点击数k，来估计一个广告或者item的点击率（比如作为统计特征加到模型里）。我们把这个要估计的点击率，作为点击率预估模型的唯一参数，接下来我们分别用MLE，MAP，贝叶斯推断来估计这个参数和使用这个参数来对点击率进行预估。也会引出工作中经常用到的贝叶斯平滑方法（很多人可能不知道，它其实是完整应用了贝叶斯推断推导出来的）

（1）MLE

首先，我们需要对似然率建模 建模，很自然的选择是Bernoulli分布（Bernoulli分布是Binomial在n=1时候的特例），Bernoulli分布就是专门用来刻画这类问题，它唯一的参数就是点击率 。

下面我们用MLE来做参数估计（训练得到  的值），当n>1时，Bernoulli分布就变成了Binomial分布，我们把它展开就是:

其中 是常数，对于计算argmax来说可以直接忽略。再用一下算法从业人员的老朋友: 取log操作。因为log是单调函数，取log不影响计算 

对上面这个式子取导数，令导数为0，就可以知道当

的时候，上面的式子可以取到最大值。

这个式子的意思就是，对于点击率预估，如果用MLE的方法，就用点击数除以展现数就好了。所以我们平时从直觉出发得到的结论，其实是有理论支撑的。不过如果点击数是1，展现数是2，我们用MLE估计出来的点击率就是0.5。一方面这个值很可能是偏高的（这个偏高是因为凭借我们对业务的理解，大概知道这个点击率比如说是在0.1左右），另外一方面是这个0.5的预估的不确定度是比较高的（比较不准的）。解决第1个预估偏高的问题，我们可以通过MAP把先验信息引入来解决。

（2）MAP

MAP和MLE的区别在于，最大化的不是似然率，而是似然率乘以先验。在这里，我们先验选择的是Beta分布。似然率分布还是和MLE的一样。

 ， 

只所以做这样的选择，是因为Beta分布是Binomial分布的共轭先验(Conjugate Prior)。什么叫共轭先验呢？请看下面的公式（其中  函数叫Gamma函数，后面我们再介绍这个函数有什么性质）

我们把Binomial分布和Beta分布都展开，就会发现一开始Binomial分布是  的形态(a,b,c都与  无关），与Beta分布相乘之后，还是的形态（只是c, a, b的值不一样了。只要满足这个性质，我们就可以说Beta分布是Binomial分布的共轭先验。共轭先验的最大的好处就是：好计算。当我们把计算出来的后验当成下一次迭代的先验的时候，再乘以下一次迭代里的似然率，得到的还是的形态，可以一直迭代下去，计算非常的方便。所以很多时候，某些分布（或者模型结构）的选择，不一定都是因为这个分布或结构贴合当前的问题，有的时候纯粹就是为了好计算。其他常见共轭分布可以见（wiki链接：https://en.wikipedia.org/wiki/Conjugate_prior）。

类似MLE里的计算，我们依次对argmin的式子进行忽略前面的常数，取log，再求导数，令导数为0。就可以求解出

这里的  和  是先验分布的参数，从直觉上，我们也可以理解为  是虚拟的正样本数，  虚拟的负样本数。例如如果 和 分别选择为11和91，那么如果在一个展现和点击也没有的时候，上式等于  ，也就是说先验知识告诉我们，如何没有任何数据，那么点击率的先验在0.1左右。当n和k的数字逐渐增大，  和  的值影响就会越来越小，逐渐收敛到  。

（3）贝叶斯推断（Bayesian Inference)

最后是贝叶斯推断。先验分布，似然率分布还是和上面MAP的保持一致。

 ， 

和MAP不一样的是，我们不是求让后验最大的  值，而是直接计算后验分布。回顾一下后验的公式是这样的。

MAP阶段之所以不用担心  的计算是因为我们是求  ， 和  无关所以可以不用管。但是现在要求完整的后验分布，就不能不管了。我们把似然率和先验分别展开，然后把和  无关的因素都提出来到前面，就有了下面的式子。

也不知道是巧合还是Beta分布设计的时候故意的，居然这个积分有下面的性质

第一类欧拉积分 

于是我们的  就可以简化成下式

接下来，我们就可以计算后验  ，并把上面的式子代入，并约掉几个分子和分母都出现的子项，就有

到这里后验分布 就算出来了，可以看到后验还是形如 。这就是共轭先验带来的好处。

第三步是计算预测值的分布，因为我们观测到D后的预测值分布  是参数为 的Bernoulli 分布，因此预测值y的分布就是  的分布。好吧，严谨点证明如下：因为y只有0和1两个取值，因此根据离散分布的期望值计算公式

到这里其实已经得到了想要的预测值的分布。

第四步就可以计算预测值的均值（或者方差了，方差就可以表示不确定度，但做贝叶斯平滑通常我们只使用均值）

翻开大一微积分课本，找到均值计算公式如下

又碰到了刚遇见的朋友：第一类欧拉积分，代入后有

这个时候还需要介绍  函数的一个性质，  ，则有

经过这么一堆复杂的积分计算，结果居然如此优雅，这就是数学的魅力吧（需要设计一个如此精巧的beta函数）。就像不管内心多么复杂的女神奥黛丽赫本，永远都是那么优雅从容。

和MAP类似，我们也可以理解为  是虚拟的正样本数，  是虚拟的负样本数。上面这个式子，也叫贝叶斯平滑，大家很可能已经在工作里用过，但是可能不知道它其实是完整应用了贝叶斯推断推导出来的。

假设 和 分别选择为10和90，那么如果在一个展现和点击也没有的时候，上式等于  。也就是说先验知识告诉我们，如何没有任何数据，那么点击率的先验在0.1左右。如果有20个点击（k=20)，100个展现（n=100)，则点击率为  。我们可以看到经过贝叶斯平滑后的点击率是介于先验点击率0.1和似然点击率0.2（20/100）之间。当n和k的数字逐渐增大，  和  的值影响就会越来越小，逐渐收敛到  。

我们可以发现，这里的  控制平滑结果是更相信先验还是更相信似然点击率：  越大，表示越相信先验，也表示需要更多的观察数据（展现和点击数）才能让结果偏离先验；而  则控制了先验的率是多少。

总结一下，用这三种方法去做  的参数估计（也等于率的预估值），结果为

在推荐和广告系统里，贝叶斯平滑可能是对各种CXR的统计类特征进行平滑最实用的方式。如果你还没有用过，那么赶紧加入到你的工程师随身携带工具箱吧。

对于 ， 这两个分布参数的选择，不是本文的重点，因此本文只介绍一个最简单其实也足够实用的方法：矩估计。查询下beta分布的wiki页面（链接：https://en.wikipedia.org/wiki/Beta_distribution），会找到它的均值和方差分别是：

均值：

方差： 

然后我们直接对我们拥有的样本，统计样本均值（计为Mean）和样本方差（计为Var），然后令

 ，  ，

然后解这个关于  的方程组，就可以算出  的值了：

有朋友可能会问，用来估计样本均值和方差的样本哪里来？我们不是要用贝叶斯平滑来平滑点击率，就说明我们没有足够多的展现和点击啊。答案是用其他场景的统计样本来估计，例如要平滑某个新广告单元下的点击率，可以用这个账户历史所有广告单元的样本来估计参数；又例如要平滑某个用户的点击率，可以用所有用户的样本来估计参数。

讲到这里，我们终于把贝叶斯推断讲完了。不过通常贝叶斯推断不能像贝叶斯平滑这样优雅地直接推导出后验分布，因为如果我们不是选择了比较简单的Bernoulli分布来建模和选择Beta共轭先验，刚好利用了这两个分布的特性（第一类欧拉积分），那么在第三和第四步的两个积分计算会很难求。因此我们需要借助一些近似算法来解决更加通用的情况，例如（中）（下）篇要讨论的蒙特卡洛采样法和变分推断的方法。（下）篇中也会对实际应用中的一些问题进行讨论。

（最后，友情提示：不要像文章封面图片中的女孩那样坐在悬崖边的栏杆上，增加了太多的不确定度）

还是广告

又到了招聘旺季，我们正在大力寻找志同道合的朋友一起在某手商业化做最有趣最前沿的广告算法，初中高级广告算法职位均有HC（迅速上车，还能赶上上市）

作者个人微信（添加注明申探社读者及简单介绍）：

欢迎扫描下面二维码关注本公众号，也欢迎关注知乎“申探社”专栏