韩非分金币：博弈论在广告竞价中的应用（下）

这是我寄几的第 58 篇文章

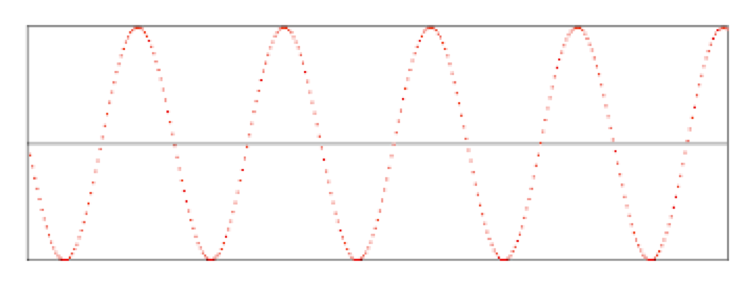
博弈论提供了一套思维框架，可以凭借逻辑来技术性地分析一些现实问题。如今互联网时代的发展让大数据的处理效率也越来越惊人，Google、Facebook等平台的收入都是靠竞价广告，而竞价就是一个博弈论的重点研究对象，设计一个好的竞价机制是直接影响这些平台的收入的，这也是一个博弈论的重要应用价值。

不同的竞价机制下，最终的均衡点效果是不尽相同的。

比如在GFP模式下，选择广告展示的过程中，就是不同的买方之间进行不断的重复博弈。在每一轮拍卖结束后，广告主会根据上一轮报价的情形决定下一轮的报价决策，这场价格战会被自然而然地分为价格上涨和下降两个阶段不断交替出现。对于广告平台来说，总收益则偏小（参考高中正弦函数等知识点，随着时间的增长，积分面积小于均衡点面积）。

在GSP的模式下，竞价的广告主由于想竞拍到广告位，且付出的是第二位的出价金额，基本都会给出自己能接受的略高的报价，报价意愿相对真实且能达到相对均衡的状态，但竞价的结果不一定全局最优的。这种情况下，广告平台的收益得到了有效的保证。

在VCG的模式下，对于赢得广告位的广告主而言，价格调整带来的成本降低不足以弥补因此减少的展示价值。此时，真实出价才是最优策略，而对于平台收益方和各广告主之间也将会处于纳什均衡状态，也就是一个占优战略均衡点。

通过不同的出价机制，得到的博弈结果也各不相同，不过仍然可以从理论的角度帮助我们优化师认识到，不同的竞价机制下，出价的策略是需要有所不同的，Google的GSP模式下，出价偏高会帮助我们获得更多机会，而Facebook的VCG模式下，真实出价将会对我们更加有利。不同的广告平台的出价特点也会帮助我们更有效的利用好广告预算。

总的来说，竞价广告的设计有很多拍卖和博弈论相关的基本理论。不仅是竞价机制，如何优化出价策略，如何分配预算，如何优化转化效率等也是值得不断思考的地方。

最后，谜底揭晓时间，之前的最开始的那个分金币问题，韩非提出的方案是：A是99枚金币，B是1枚金币，而C是0枚。